Ramsey's theory
이 이론은 순서가 나타나야 하는 조건을 연구하는 수학 분야이다.
Ramsey's theorem
Ramsey Theory
한국말 없니?
램지의 정리(영어: Ramsey’s theorem)는
충분히 큰 완전 그래프의 변을 색칠할 경우,
동색의 클릭을 찾을 수 있다는 정리이다.
5각형
이것을 전체집합으로 보고
점과 점을 연결해서 만들어진 도형.
이것의 각 각을 하나하나의 부분집합
일단 정리가 안 되니까 가본다. 가다 보면 나오지 않을까?
이 이론 자체가 그 부분집합이 크기가 m인 부분집합
크기가 같은 도형들의 집합을 (m 위에 S) 일단 급하니까. ㅎ
이때 m이란 것은 초변의 크기
아, 무슨 부분집합을 계속 쪼개 들어가지?
음.
집합 S⊇(m 위에 S) 전체집합인 S가 크다.
m초 그래프는 5초 그래프라고 표현을 하자!
초변의 크기라는 것이 꼭지점의 갯수이다.
이 5초 그래프는 부분집합을 가진다.
그리고 초변의 수는
부분집합 들의 개수이다.
점과 점들을 이어서 만들어진 작은 도형들의 개수이다.
왜 이 이론을 도형에 가져다 붙여 놓았지?
복잡하게 만든 이유가 있을 것 같은데
복잡한 것이 아닌데? 그 당시에는 이것밖에 없었다?
뭐야 자명한 경우?
도대체 지금까지 뭘 본 것이지? ㅋ
m이 1일 때, S≡ (m 위에 S)
점 하나가 S이고 자기 자신이다. 점이 하나밖에 없으니까!
자신이 전체집합이면서 동시에 부분집합이다.
그러면 둘인 경우는?
증명하는 방법인가?
m이 1일 때 조건을 만족한다.
m이 2일 때 조건이 만족한다.
... m이 c까지 갈 때도 만족한다.
c, 양의 정수이다. 어떤 수라도 상관없다.
5면 5, 10이면 10, 100이면 100, 무한도 성립한다.
일단 여기까지만!
일부터 해야 함. ㅡㅡ/ 정지!
어떻게든 이해를 해야지. 나는 꼭 알아야 한다.
죽일 놈의 수학, 사랑하기로 마음을 바꿨음. ㅎ
수학아, 나 좀 도와주라! ㅡㅡ. 제발요. 유유.
정중하게 부탁했음. ;; 숨막혀 죽겠다! ㅋ
어제 밥 한 그릇 먹었는디? 또 배고프네? 이그!
01:39
마방진! 아. 아. 감사!
그래서 도형이었어요!
잠시 딴 짓하다 다시 보니 보이네? 크.
http://math.kongju.ac.kr/math/main/data/story1/1obdz.html?ckattempt=1
마방진이란 가로, 세로, 및
대각선에 있는 각각의 합이 같도록 배열한 사방팔방 도형이다.
마방진에 쓰이는 숫자는 중복하여 쓰면 안 되고,
자연수를 꼭 한 번씩만 써야 한다.
따른 수의 합은 3방진은 15, 4 방진은 34, 5방진은 65, …,
n방진은 n(n2+1) / 2 이다.
이것만 이렇게 접근하고 초딩부터 다시 가겠습니다. 수학님.
배우는 순서, 내 방식으로 간다. 굉장히 빠르다.
영문권 포함 웹을 모조리 뒤져 문제풀이 방법의 다양성을 확보할 생각이다.
사전을 조금 뒤져야 하여 그렇지 원서는 볼 줄 안다.
이것 볼 줄 모르면서 이런 것 안 푼다. 단지 수학만 모른다.
1+1=?
번역하면? 일(Work) 더하기 일(Work)은? 일에 치여 죽는 것!
얼마 전에 SIR 자게에서 봤다. ㅡㅡ
다양한 방법으로 접근하는 눈을 키우고 싶다. ㅡㅡ
웹을 통하여 배우고 싶은 이유. < 검색하다 느낀 점이다.
내가 수학 꼴통이잖아? 진짜 수포자 맞고!
그래서 이야긴데 만약 내가 수포자에서
추상대수학을 서술 할 수 있는 과정까지 올라가는 코스를
영어로 담으면 장사가 좀 될까? 이런 컨텐츠 승산이 있겠냐는 것이지.
어차피 나는 배워야 하고? 과정을 담아? 돈도 벌고! ㅋㅋㅋ
뭐를 해도 좋은데 세계 1등만 하고 싶거든요? ^^
3차 접근 성과는 만족하지만
마방진을 모르네? 아흐.
뭔지만 알았지 아직 모름. 갈 길이 정말 머네…
밥 묵고 가야지 가다가 쓰러지면 안 되잖아? 고맙다 구글이!
/////////////////
비둘기 집의 원리와 램지 이론
이것을 쳐다보았으나 왜 순서가 필요하지 모르겠다.
2017.08.10. 16:46:28
Ramsey Theory
순서까지 모두 들어있다. 램지 이론이다.
2017.08.10. 19:20:03 (10분)
비둘기 집의 원리가 램지의 정리다.
우리 집에 방이 2개가 있다. 그런데? 아이는 3명이다.
이 세 명에게 방 두 개를 나눠서 쓰라고 한다.
그러면 분명히 어느 방에는 두 명이 들어갈 수 있다.
두 명 이상, 세 명이 들어갈 수도 있다.
이 점 세 개를 놓고 봤을 때, 어느 것 두 개 이상은 같은 색을 가진다. 동색.
5각형, 점 다섯 개를 놓고 봤을 때도 똑같다.
점이 많아져도 이 이론과 똑같다.
방이 10개 일 때, 아이 11명에게 너희가 들어가고 싶은 대로 들어가!
각각 한 명씩 들어갈 수도 있다. 10방까지 모두 찼다.
하지만 11번 아이는 이미 방을 차지하여 어딘가로 들어가야 한다.
그래서 어느 방에는 이 아이가 들어감으로써 두 명 이상이 존재하게 된다.
또는 어느 방 하나에 몽땅 들어갈 수도 있다.
말은 표현은 부분집합이 존재한다고 했는데
비둘기 집의 원리를 수식으로 바꿔 표현한 것이 램지 이론의 기본인 것 같다.
이 이론은 도형만 되는 것이 아니다.
비둘기 집이고, 도형이고, 어떻게 보면 참여자 수를 추측하거나
순열조합, 확률, 모든 것이 다 들어있는 것 같다.
'이 이론은 순서가 나타나야 하는 조건을 연구하는 수학 분야이다.'
여기만 아직 모르겠다. < 나는 느리다. 하지만
흐흐 얼마 안 남았음. ㅡㅡ 재밌네. ㅜㅜ
이미 답은 나와있다. 한글이다.
도저히 못 알아 본다면 그때 보겠음. 감사!
///////////////////////////////////////////////
램지 이론과 당장은 상관이 없음.
광고창이 떴길래 궁금해서 찝적거림. ㅡㅡ
그런데 이거 뭐니?
Can you make this equation true?
6□3□3=3
6+3/3=3 < 이런 방법은 혼합계산 방법에서 틀린 것 아니니?
(6+3)/3=3 < 이것이 맞지 않니?
다른 것인가? 사칙연산이 아닌 다른 것. 오 재밌네?
새벽에 고민해 보겠음. 엄청 재밌다. ㅋ
Party Hefty!
Creating new ways to see the world. It's awesome.
.........................
2017.08.11. 07:24:35 (10분)
수학 자체가 모두 순서네?
밑변 곱하기 높이 나누기 2 삼각형의 넓이 이것도 순서가 있다.
그런데? 이것보다 더하기 곱하기 나누기 뺴기가 막 섞여있는 경우는
우선순위를 줘야 한다. 이거구나. 오!……
이미 순서가 다 정해져 있었던 것이다. 오호 이런!
초딩학교 수준인디 이것을 이제 알다니. ㅋ
아무리 느려도 그렇지. ㅜㅜ 어떻게 이렇게 느리니!
6□3□3=3
이 방정식을 성립시킬 수 있는 방법은?
루트를 씌우면 되지만 그래도 모양이 안 맞고
가로나 루트나. ㅡㅡ
수학도 별 것 없네. ㅡㅡ ㅎㅎㅎㅎ
어렵다는 것 누구보다 잘 안다. 어렵다 생각하면 어떻게 배우겠니!
쉽다고 생각은 절대 안 한다. 쉬우면 재미없거든. ㅡㅡ/
사칙연산이 엄청 중요하구나. 가장 기본!
문제는 풀지 못했다. 대신
수학은 순서가 이미 정해져 있다는 사실만 알게 된다!
램지 이론은 아직 더는 못 봤다.
내가 느리잖아? ㅋ
원래 빨리 빨리 못한다. 제대로 뜯고 싶다!
2017.08.11. 07:56:56
너 정말? ㅡㅡ
이건 또 뭐니?
ㅡㅡ/
빨래도 해야 하고 할 것 많다. 점심 때 붙겠음!
이 인간이 미쳤나? 수학공식만 보이네? ㅎㅎ
제곱근표 제대로 된 것 하나 부탁한다.
알아야 풀지! ㅜㅜ (참고하여 보려고 함)
거꾸로 갈 생각이다. 225에서 출발.
이거 아니었음.
2017.08.11. 09:30:20
루트 121
전체 총 30분 걸린 것 같다.
틈틈히 생각하다가 숫자로 넣어서 풀어 본 것은 약 3분~5분?
처음에는 단순한 숫자라고만 생각했다.
그런데? 숫자라고만 생각하니까. 앞에 있는 루트x + 15 이놈이
단순한 자연수로 빠져 나오지 않는다.
그래야 = 15가 될 수 있는데 말이다.
될 수 없었어요.
그래서 다시 생각한다.
어쨌든 자연수 15는?
x 자체가 제곱근을 벗고 나와봐야 할 것 같더라고?
그래서 더하기 15하고 자연수로 나오게끔 한다.
그러다 보니까?
루트 121이 자연수 11곱하기 11이다.
제곱근 표는 안 봤다.
볼 필요가 없었다. 내가 제곱근표를 보려고 한 것은
루트3 같이 제곱으로 못 벗는 애들을 보려고 했다.
어?
지금 다 틀렸다?
잘못 생각했네? 어잉. 이거 엄청 어렵네?
못 풀었네? 헐. 망했네. ㅡㅡ
어? 딱 맞았는데? 헐.
다시 붙겠음. ㅜㅜ
..................
2017.08.11. 09:41:17
x=49
방정식으로 풀면 되는 것을 왜 자꾸 숫자와 사칙연산에 집착했을까.
x는 미지수였는데!
10초 안 걸린다.
재밌네. 수학이란 놈 재밌다.
선입견이 무섭다. x가 들어가면 방정식으로 푼다!
하나 배웠음. 미지수 x는 방정식이 가장 빠르다.
하지만? 그렇다 해도 못 푸는 애들이 있잖아?
다음에 생각할란다.
못 풀 때는 1대1 대응으로 풀면 되더라고?
시간이 엄청 걸리지만! < 나는 이런 것도 지겹지 않다.
다음 문제 없니?
아 사칙연산 해결 못했네?
설마 답이 가로를 치는 것은 아니겠지?
방정식으로 풀어야 할 것을 '수치대입법'으로 푼다.
이러니 내가 얼마나 느리겠는가!
이제 조금 빨라진 기분이 드는 군. ㅋ 고맙다!
/////////////////
(m 위에 S) < 이거 어떻게 표기해야 해요?
어렵네요. ㅡㅡ
이렇게 생겼습니다.
/////////////////
뜯을시간이필요합니다.

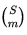


댓글 4개
저는 마방진까지 접근하는데 무려 몇 시간이 걸렸습니다. ㅡㅡ 흑.
속이 뭉그러집니다. ㅎㅎ 그래도 할 겁니다. ^^
일단 저장.
....................
2017.08.10. 07:19:02
잠만 잤다. 이렇게 하여 무엇을 배우겠는가 싶다.
3차 접근 이후 더 접근도 못 하고, 링크 속 마방진은 구경도 못 한다.
현실, 이제 배워서는 늦습니다.
현실, 그렇다 해도 마땅히 뭘 할 것도 없는 나, 놀 수는 없으니 배우고 싶다.
현실, 잤다. 무려 10시간을……
현실, 오늘 꿈은 수학 공식이 사라진 다른 꿈이다. 꿈마저도 협조를 안 한다.
현실, 나는 못 배운다! 잉?
현실, 그런데 행복하다. 이 기분은 왜 이 모양일까?
.......................
2017.08.10. 07:51:27
비둘기 집의 원리와 램지 이론.pdf 문서를 지금 본다.
비둘기 집의 원리가 램지이론이다.
이것을 보면? 뭔지는 알 수 있을 것 같다. (1분 소요)
.........................
2017.08.10. 16:31:14
비둘기 집의 원리와 램지 이론
http://mathsci.kaist.ac.kr/~sangil/home/wp-content/uploads/2015/01/pigeon.pdf
램지의 정리에서 출발하여 비둘기로 왔거나
비둘기 집을 보고 정리가 시작되어 이런 예제들이 생긴 것 같다.
시작과 끝이 점점 확대되는 정리방법이다.
''이 이론은 순서가 나타나야 하는 조건을 연구하는 수학 분야이다.'
규칙을 가지고 있다는 의미인데?
어딘지는 아직 모르겠음.
(약, 20분 소요 됨)
이 이론이 시작하게 된 시점부터 봤으면 좋겠는데. 없을까?
안에 들어있는 공식도 이제는 조금 알겠는데 그래도 모르겠다.
전체 공식 없을까? 처음부터 여기까지 온 과정 같은 것?
이거, 행렬로 커버가 안 되는 곳을 증명할 수 있는 방법같지 않니?
공식 전체가 필요함.
이미 담아 놓고도 내 눈이 그렇지 ㅡㅡ/
http://people.maths.ox.ac.uk/gouldm/ramsey.pdf (램지 이론)
이 속에 모두 들어있었는데 왜 이것이 지금 보이지? ㅡㅡ
모르면 안 보이는군. 신기하네 ;
따식 모르면서도 본능이 뭔지 챙겨 올 것은 모두 잘 챙겨왔어요. ㅋ
저도 얼마 전에 알았습니다. ㅋ
제곱이 아니네요? 잉.
아직 몰라요. ㅎ
어떻게 하는지 방법은 아는데요. 코드는 못 외웠어요!